El Número Φ: La Proporción Divina
El número \( \phi \) (phi), aproximadamente igual a 1.61803, es conocido como la proporción áurea o divina proporción. Esta constante matemática ha fascinado a artistas, arquitectos y matemáticos durante siglos por su presencia en la naturaleza y su belleza estética.
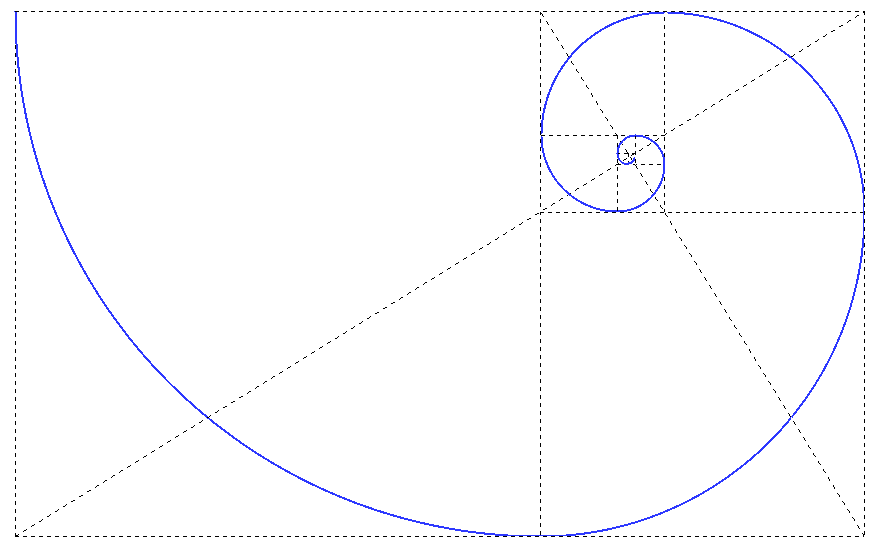
Representación visual de la proporción áurea
¿Qué es la proporción áurea?
La proporción áurea es la relación entre dos cantidades \( a \) y \( b \) donde:
Esta proporción puede expresarse algebraicamente como:
Propiedades Matemáticas
El número \( \phi \) tiene propiedades matemáticas fascinantes:
- Es solución de la ecuación \( \phi^2 = \phi + 1 \)
- Su inverso es \( \phi^{-1} = \phi - 1 \approx 0.61803 \)
- Relación con la sucesión de Fibonacci: \( \lim_{n \to \infty} \frac{F_{n+1}}{F_n} = \phi \)
- Expresión como fracción continua: \( \phi = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}} \)
- Raíz anidada: \( \phi = \sqrt{1 + \sqrt{1 + \sqrt{1 + \cdots}}} \)
La Proporción Áurea en el Arte y la Naturaleza
1. Arte y Arquitectura
Desde el Partenón en Grecia hasta las obras de Leonardo da Vinci, la proporción áurea ha sido utilizada para crear composiciones estéticamente placenteras.
2. Naturaleza
Aparece en la disposición de hojas en plantas (filotaxis), en la concha del nautilus, en la forma de galaxias espirales y en las proporciones del cuerpo humano.
3. Diseño Moderno
Muchos logotipos corporativos, diseños de productos y formatos de pantalla utilizan proporciones cercanas a la áurea por su atractivo visual.
Curiosidades Históricas
La proporción áurea fue estudiada por los antiguos griegos, pero fue Luca Pacioli en 1509 quien la denominó "Divina Proporción" en su libro. Johannes Kepler la describió como "una joya preciosa" de la geometría.
Esta constante aparece en lugares sorprendentes, desde las proporciones de la Gran Pirámide de Giza hasta las obras de Salvador Dalí en el siglo XX.
